Software
Gridap.jl (Role: Project leader)

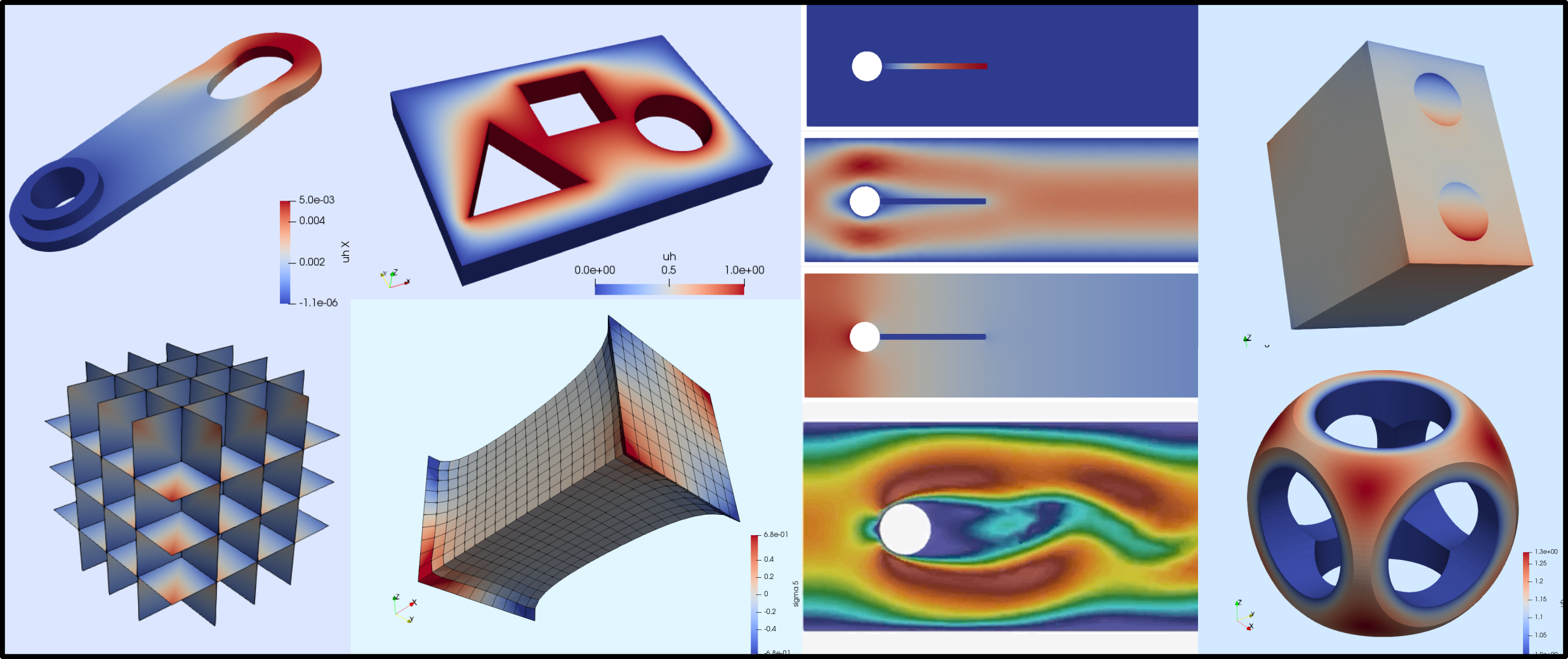
Gridap.jl is a free and open source FE library exclusively written in Julia. It is a general-purpose library which, rather than providing pre-bluid solvers for particular equations and methods, it makes available a feature-rich set of tools that allows users to build advanced solvers for their particular needs. With Gridap.jl, one can easily prototype FE methods in a laptop and eventually deploy them in large HPC clusters, with virtually no modifications of the high-level user code, and without departing from Julia code (i.e., no knowledge of C/C++ or fortran required at any point of the workflow).
The library currently supports linear and nonlinear PDE systems for scalar and vector fields, single and multi-field problems, conforming and nonconforming FE discretizations, on structured and unstructured meshes of simplices and n-cubes. Gridap.jl is extensible and modular. One can implement new FE spaces, new reference elements, use external mesh generators, linear solvers, post-processing tools, etc. See, e.g., the list of available Gridap.jl plugins.
More info:
Visit the official Gridap.jl Github repository.
To get started, take a look at the Gridap.jl Tutorials.
Ask us anything in our Gitter chat.
I am an essential contributor to the project since early 2020 (e.g., 3rd in number of commits). I have acquired a deep understanding of its internals, and developed/improved some major components of it, mainly those related to extending it towards distributed memory parallelism and hybridizable finite element discretization schemes. I have also written several tutorials, including a major one for developers, which goes over its internals, and it is an essential resource to computational math researchers that want to leverage the package for their own research.
GridapHybrid.jl (Role: Project leader)
GridapHybrid.jl is a fresh approach, based on Julia, towards a unified computational framework that supports R&D in hybrid discretization methods on general polytopal meshes, including HDG, HHO, and VEM, and highly scalable parallel preconditioning techniques (based, e.g., on hybrid multiscale ideas) tailored to these discretization techniques. By wisely leveraging the 21st century features of Julia, GridapHybrid.jl strikes a remarkable balance between computational performance, user-experience and work-flow productivity. (e.g., it releases the user from writing nested loops over mesh objects, quadrature points, trial and test shape functions). In contrast to other similar-in-spirit frameworks (such as, e.g., SLATE-Firedrake) GridapHybrid.jl does not depend on a rigid domain specific language and a compiler of variational forms; form compilers are sophisticated systems not designed to be extended by average users, e.g., to support general polytopal meshes. Besides, both front-end and back-end are written in the same programming language (Julia), circumventing the two language problem (e.g., a Python front-end for rapid prototyping and a C/C++ back-end for performance). As a matter of fact, an efficient primal HHO program for the Poisson problem can be written, using a high-level compact interface provided by GridapHybrid.jl, in less than a hundred lines of code. I have also implemented the back-end which provides support to this interface. It follows the dimension-independent construction of the method, and thus can be applied to arbitrary-dimensional PDEs. Besides, with GridapDistributed.jl (see below), parallelization of HHO (or other hybridizable method) is straightforward. Without sacrificing performance, the code follows mathematical abstraction to an extent that the formal language of mathematics is enough to write programs with these tools (a minimal number of extra coding artifacts have to be learned). This has an evident impact on productivity, and also in the adoption of R&D methods by domain scientists and practitioners.
GridapDistributed.jl (Role: Project leader)
GridapDistributed.jl is a registered Julia software package which provides fully-parallel distributed memory data structures and associated methods for the FE numerical solution of PDEs on parallel computers. Thus, it can be run on multi-core CPU desktop computers at small scales, as well as on HPC clusters and supercomputers at medium/large scales. The data structures in GridapDistributed.jl are designed to mirror as far as possible their counterparts in the Gridap (see below) Julia software package, while implementing/leveraging most of their abstract interfaces. As a result, sequential Julia scripts written in the high-level Application Programming Interface (API) of Gridap can be used verbatim up to minor adjustments in a parallel distributed memory context using GridapDistributed.jl. This equips end-users with a tool for the development of simulation codes able to solve real-world application problems on massively parallel supercomputers while using a highly expressive, compact syntax, that resembles mathematical notation. This is indeed one of the main advantages of GridapDistributed.jl and a major design goal that we pursue. For more details, go to GridapDistributed.jl github repo page. For a recent overview of the project, please see the following reference:
Santiago Badia, Alberto F. Martín and Francesc Verdugo.
GridapDistributed: a massively parallel finite element toolbox in Julia.
Journal of Open Source Software, 7(74), 4157, 2022.
DOI: 10.21105/joss.04157
GridapGeosciences.jl (Role: Project leader)

GridapGeosciences.jl is a test-bed software framework written in Julia for R\&D on numerical methods for geophysical flows, with application to NWP models, such as the non-linear rotating shallow-water equations and the 3D Euler compressible equations. I am developing this package in the framework of a collaboration with Dr. Justin Freeman (manager of the Model Systems team) and Dr. David R. Lee (staff scientist) from the Australian Bureau of Meteorology. The animation above was computed with GridapGeosciences.jl in the Australian Gadi supercomputer, and shows the magnitude of the vorticity field (curl of the velocity field) associated with the solution of a turbulent benchmark for the nonlinear shallow water equations (the so-called Galewsky benchmark). Here we are solving a surface Partial Differential Equation on the Earth surface (a 2D manifold) embedded in 3D.
FEMPAR (Role: Project leader)

I am co-founder and main developer of FEMPAR, an open-source, mathematical software package for the numerical modelling of problems governed by PDEs on HPC platforms. It provides a set of state-of-the-art numerical discretizations, including finite element methods, discontinuous Galerkin methods, XFEM, and spline-based functional spaces. The library was originally designed to efficiently exploit distributed-memory supercomputers and easily handle multiphysics problems. It also provides a set of highly scalable numerical linear algebra solvers based on multilevel domain decomposition for the systems of equations that arise from PDE discretizations. In particular, it contains a novel bulk-asynchronous, fully-distributed, communicator-aware, inter-level overlapped, and recursive algorithmic adaptation of multilevel domain decomposition preconditioners towards extreme-scale computations which was shown to efficiently scale up to the 458K cores of the IBM BG/Q supercomputer installed in JSC, Germany. Thanks to these outstanding results, FEMPAR was qualified for High-Q club status, a distinction that JSC (Germany) awards to the most scalable EU codes.
The first public release of FEMPAR was almost 300K lines of code written in (mostly) OO Fortran and it made intensive use of the features defined in the 2003/2008 standards of the language. FEMPAR has successfully been used in 40x JCR Q1-ranked research papers on different topics and application areas: simulation of turbulent flows and stabilized FE methods, MHD, monotonic FEs, unfitted FEs and embedded boundary methods, AMR, AM and HTS simulations, and scientific software engineering. It has also been used for the highly efficient implementation of DD solvers and block preconditioning techniques. Its users/developers span different research groups on national and international-level institutions, including UPC, CIMNE, ICMAB-CSIC, CIEMAT, ICTJA-CSIC, Czech Academy of Sciences (Czech Republic), Sandia National Labs (EEUU), North Carolina State University (USA), Duy Tan University (Vietnam), Monash University (Australia), and l’Ecole Politechnique (Paris). Besides, it was a crucial tool for the successful execution of several high-quality EU-funded projects, namely, 1x ERC starting grant, 2x ERC PoC projects, 1x EU-FP7 project, and 3x H2020 projects.
For those who are interested on the design and rationale behind the mathematically-supported software abstractions in FEMPAR, a very through presentation is available at the following reference:
Santiago Badia, Alberto F. Martín and Javier Principe.
FEMPAR: An object-oriented parallel finite element framework.
Archives of Computational Methods in Engineering 25, 2 (2018), 195–271.
[ArXiv link] [DOI]
A very nice tutorial-driven introduction to the software library (v1.0.0) can be found at the following reference:
Santiago Badia, and Alberto F. Martín.
A tutorial-driven introduction to the parallel finite element library FEMPAR v1.0.0
Computer Physics Communications Volume 248, March 2020, 107059.
[ArXiv link] [DOI]